决策树算法的原理详细
决策树在机器学习中有着广泛的应用,主要是因为它易于解释。例如,现在要做一个决策:周末是否要打球,我们可能要考虑下面几个因素。第一,天气因素,如果是晴天,我们就打球,如果是雨天我们就不打球。第二,球场是否满员,如果满员,我们就不打球,如果不满员我们就打球。第三,是否需要加班,如果加班则不打球,如果不需要加班则打球。这样我们就形成了一个决策树,如图 1 所示。
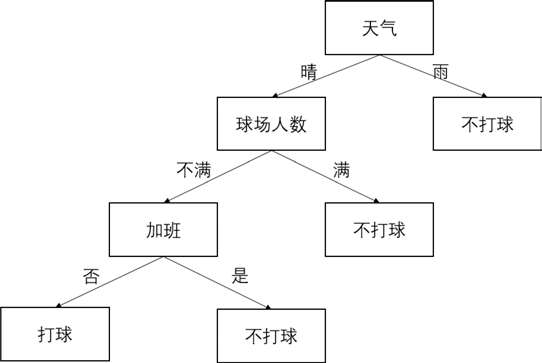
图1:是否打球的决策树
可以将这个决策过程抽象一下,每个决策点称为分支节点,如图 2 所示。
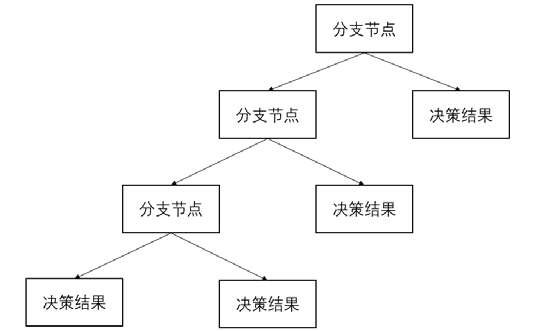
图2:抽象决策树过程
这是一个很有意思的问题,在构造决策树时,需要将那些起决定性作用的特征作为首要的决策点。所以我们要评估每一个特征,然后将它们按作用大小排列。
而这个决定性作用应该如何衡量呢?首先,要了解一个概念——“熵”。熵是指信息的期望值。信息熵的公式为:
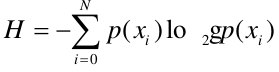 假设我们有如下数据,如表 3 所示。
假设我们有如下数据,如表 3 所示。
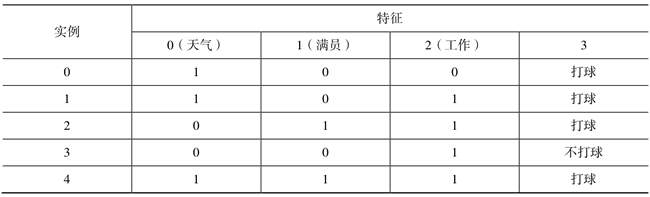
图3:是否打球的决策数据
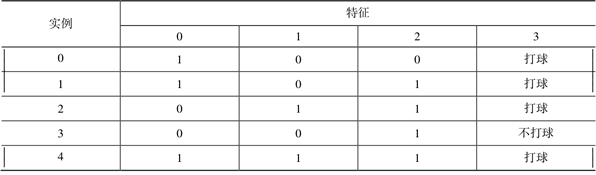
表2:特征0中数值为1的实例
同样的道理,我们可以挑选出特征 0 中数值为 0 的实例,如表 3 所示。
jid表3:特征0中数值为0的实例
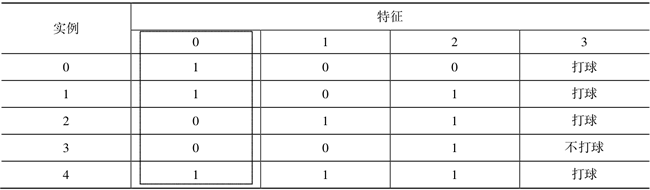
表4:选定第1列计算其信息增益
根据该列特征所包含的值将原表分割成表 5 和表 6。然后分别计算表 5 和 6 的信息熵,再用二者的熵求整个特征的熵。
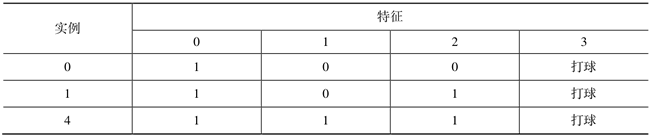
表5:表4中虚线框内特征值全为1的分为一个表

表6:表13.4中虚线框内特征值全为0的分为一个表
同样的道理,我们还可以计算出其他特征的信息熵,最后的结果如表 7 所示。

表7:各个特征的信息增益
根据特征的得分可以看到,特征 0(也就是天气)得分最高,所以我们把它作为第 1 个分支节点,同样的道理可以递归找寻下一层的分支节点。
声明:《Python系列教程》为本站“54笨鸟”官方原创,由国家机构和地方版权局所签发的权威证书所保护。

图1:是否打球的决策树

图2:抽象决策树过程
1. 信息熵
看起来很简单,但是有一个问题,如何确定决策点的顺序呢?例如在是否打球的决策树中,我们为什么会选择天气因素作为第一个决策点,而不将球场是否满员作为第一个决策点呢?这是一个很有意思的问题,在构造决策树时,需要将那些起决定性作用的特征作为首要的决策点。所以我们要评估每一个特征,然后将它们按作用大小排列。
而这个决定性作用应该如何衡量呢?首先,要了解一个概念——“熵”。熵是指信息的期望值。信息熵的公式为:
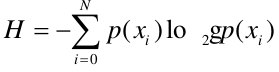

图3:是否打球的决策数据
1) 导入相关模块
In [1]: import numpy as np ...: import pandas as pd
2) 导入相关数据
In [2]: data = [ ...: [1, 0, 0, '打球'], ...: [1, 0, 1, '打球'], ...: [0, 1, 1, '打球'], ...: [0, 0, 1, '不打球'], ...: [1, 1, 1, '打球'] ...: ]
3) 将数据转换为数据框
In [3]: df=pd.DataFrame(data)
4) 查看数据的长度
In [4]: data_length = len(data) ...: data_length Out[4]: 5
5) 提取目标变量
In [5]: target = df.iloc[:,-1]
6) 计算目标变量各个类型的数量
In [6]: label_counts = target.value_counts() ...: label_counts Out[6]: 打球 4 不打球 1 Name: 3, dtype: int64
7) 将列表转换为字典的格式
In [7]: label_dict = label_counts.to_dict()
...: label_dict
Out[7]: {'打球': 4, '不打球': 1}
8) 初始化熵的值
In [8]: entropy = 0
9) 计算熵
In [9]: for key in label_dict: ...: prob = float(label_dict[key])/data_length ...: entropy -= prob * np.log2(prob)10) 查看结果
In [10]: entropy Out[10]: 0.7219280948873623
2. 分割数据
知道了如何计算信息熵,接下来就是要计算信息增益了,信息增益就是信息熵的差值。在计算信息增益之前要对数据进行分割。1) 导入相关模块
In [1]: import pandas as pd
2) 导入相关数据
In [2]: data = [ ...: [1, 0, 0, '打球'], ...: [1, 0, 1, '打球'], ...: [0, 1, 1, '打球'], ...: [0, 0, 1, '不打球'], ...: [1, 1, 1, '打球'] ...: ]
3) 创建数据框
可以看到默认 columns是 0,1,2,3,他们分别代表了 0:天气因素,1:是否满员,2:是否加班,3:目标变量。In [3]: df = pd.DataFrame(data) ...: df Out[3]: 0 1 2 3 0 1 0 0 打球 1 1 0 1 打球 2 0 1 1 打球 3 0 0 1 不打球 4 1 1 1 打球
4) 创建筛选条件
In [4]: selector = df.loc[:,0]==1 ...: selector Out[4]: 0 True 1 True 2 False 3 False 4 True Name: 0, dtype: bool
5) 筛选数据
这里筛选的是特征 0 中数值为 1 的实例。df_split = df[selector] df_split Out[5]: 0 1 2 3 0 1 0 0 打球 1 1 0 1 打球 4 1 1 1 打球我们挑选出来了特征 0 中数值为 1 的实例,如表 2 所示。

表2:特征0中数值为1的实例
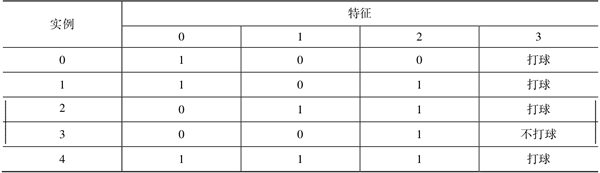
同样的道理,我们可以挑选出特征 0 中数值为 0 的实例,如表 3 所示。

jid表3:特征0中数值为0的实例
3. 计算信息增益
我们将通过信息增益来评价每个特征的重要程度。首先,将上述信息熵与分割数据的代码封装成函数,因为在计算信息增益过程中要反复用到。1) 导入相关包
In [1]: import numpy as np ...: import pandas as pd
2) 导入相关数据
In [2]: data = [ ...: [1, 0, 0, '打球'], ...: [1, 0, 1, '打球'], ...: [0, 1, 1, '打球'], ...: [0, 0, 1, '不打球'], ...: [1, 1, 1, '打球'] ...: ]
3) 封装计算熵的函数
In [3]: def ent(data): ...: df=pd.DataFrame(data) ...: data_length = len(data) ...: target = df.iloc[:,-1] ...: label_counts = target.value_counts() ...: label_dict = label_counts.to_dict() ...: entropy = 0 ...: for key in label_dict: ...: prob = float(label_dict[key])/data_length ...: entropy -= prob * np.log2(prob) ...: return entropy
4) 测试计算熵的函数
In [4]: ent(data) Out[4]: 0.7219280948873623
5) 封装分割数据的函数
In [5]: def split(data,feature_rank):
...: df = pd.DataFrame(data)
...: groups = df.groupby(by=feature_rank)
...: data_group = {}
...: for key in groups.groups.keys():
...: data_group[key] = df.loc[groups.groups[key], :]
...: return data_group
6) 测试分割数据的函数
In [6]: data_group=split(data,0)
7) 查看分割后数据的分类名称
In [7]: data_group.keys() Out[7]: dict_keys([0, 1])
8) 查看第1个分类
In [8]: data_group[0] Out[8]: 0 1 2 3 2 0 1 1 打球 3 0 0 1 不打球
9) 查看第2个分类
In [9]: data_group[1] Out[9]: 0 1 2 3 0 1 0 0 打球 1 1 0 1 打球 4 1 1 1 打球
10) 初始化原始数据的熵
以上步骤主要是函数的封装,下面正式进入信息增益的计算。In [10]: init_ent = ent(data)
11) 选定要计算的特征
这里选用第 1 列特征。In [11]: feature_rank = 0
12) 分割数据
In [12]: data_group = split(data,feature_rank)13) 初始化将要计算的熵的值
In [13]: new_ent = 0
14) 计算该特征的信息熵
In [14]: for key in data_group:
...: prob = len(data_group[key])/len(data)
...: new_ent += prob*ent(data_group[key])
15) 得到信息增益
In [15]: info_gain=init_ent-new_ent
...: info_gain
Out[15]: 0.3219280948873623
接下来,通过实例看一下如何计算特征 0 的信息增益。首先选择表 4 中虚线框内的列。
表4:选定第1列计算其信息增益

表5:表4中虚线框内特征值全为1的分为一个表

表6:表13.4中虚线框内特征值全为0的分为一个表
同样的道理,我们还可以计算出其他特征的信息熵,最后的结果如表 7 所示。

表7:各个特征的信息增益
声明:《Python系列教程》为本站“54笨鸟”官方原创,由国家机构和地方版权局所签发的权威证书所保护。
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: