决策树(Decision Tree)基本概念:概率与期望
决策树又称为判定树,它所使用的知识包含概率、期望以及信息熵。顾名思义,决策树方法就是对一件事做出决定,比如我们该执行方案 1,还是方案 2。但用决策树方法做出决策并不是去考虑具体的因素,而是有一定的信息理论支撑。比如有关概率和期望的知识,以及信息理论中的信息熵和信息增益的概念。
首先我们要先了解决策树方法需要的基本知识——概率与期望。
信息值,可以简单理解为信息的价值。什么样的信息是有价值的呢?假如你生活在平原,我告诉你,明天不会地震。这个信息的价值就很低,因为发生地震的概率本来就很低。但是,如果我告诉你,明天会发生地震,这个价值就很高了,因为我预测了一个小概率事件。对,这就是信息价值的定义,概率越小的信息,价值越高。我们用以下公式表达信息的价值。
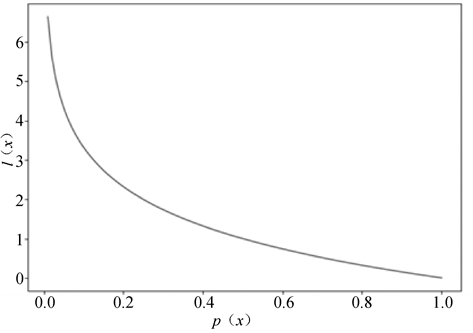
图1:信息值与概率之间的关系
可以看到随着概率值的增加,信息值在降低。
声明:《Python系列教程》为本站“54笨鸟”官方原创,由国家机构和地方版权局所签发的权威证书所保护。
首先我们要先了解决策树方法需要的基本知识——概率与期望。
概率与期望
数学期望是实验中每次可能结果的概率乘以其结果的总和。比如在我们购买彩票的时候,5 元面值的彩票的中奖概率是 0.4,不中奖的概率是 0.6,那么我们购买彩票获奖的期望就是 5×0.4+0×0.6=2 元。信息值,可以简单理解为信息的价值。什么样的信息是有价值的呢?假如你生活在平原,我告诉你,明天不会地震。这个信息的价值就很低,因为发生地震的概率本来就很低。但是,如果我告诉你,明天会发生地震,这个价值就很高了,因为我预测了一个小概率事件。对,这就是信息价值的定义,概率越小的信息,价值越高。我们用以下公式表达信息的价值。
l(xi)=-log2p(xi)
1) 导入相关模块
这里我们使用了 math 模块。math 模块包含了基础数学计算的包。In [1]: import matplotlib.pyplot as plt ...: from math import log
2) 生成p(x)
In [2]: x = [i/100 for i in range(1,101)] ...: x Out[2]: [0.01, 0.02, 0.03, 0.04, 0.05, 0.06, 0.07, 0.08, 0.09, 0.1, ...... 0.9, 0.91, 0.92, 0.93, 0.94, 0.95, 0.96, 0.97, 0.98, 0.99, 1.0]
3) 生成l(x)
In [3]: y = [-log(i,2) for i in x] ...: y Out[3]: [6.643856189774724, 5.643856189774724, 5.058893689053569, 4.643856189774724, 4.321928094887363, 4.058893689053568, 3.8365012677171206, 3.6438561897747253, 3.4739311883324127, 3.321928094887362, ...... 0.15200309344504997, 0.13606154957602837, 0.12029423371771177, 0.10469737866669322, 0.08926733809708741, 0.07400058144377693, 0.058893689053568565, 0.043943347587597055, 0.029146345659516508, 0.01449956969511509, -0.0]
4) 作图
信息值与概率之间的关系如图 1 所示。
In [4]: plt.xlabel("p(x)")
...: plt.ylabel("l(x)")
...: plt.plot(x,y)
Out[4]: [<matplotlib.lines.Line2D at 0x8eeba90>]

图1:信息值与概率之间的关系
可以看到随着概率值的增加,信息值在降低。
声明:《Python系列教程》为本站“54笨鸟”官方原创,由国家机构和地方版权局所签发的权威证书所保护。
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: