神经网络算法实战:MLPRegressor回归
MLPRegressor 主要用来做回归,现在来测试一下用模拟数据做回归模型的效果。
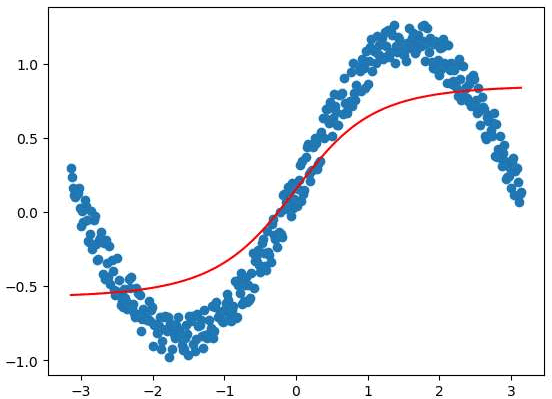
图1:回归神经网络结果
我们还可以尝试用不同的激活函数得到不同的结果,如图 2 和图 3 所示。
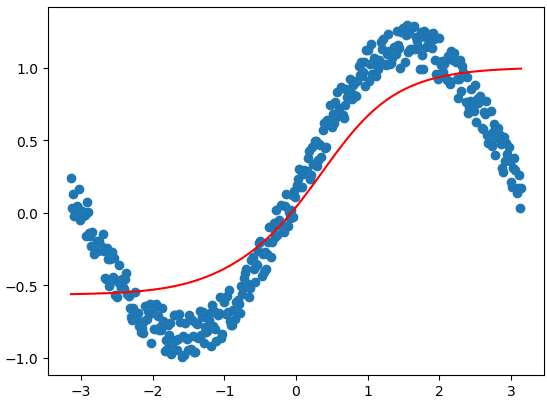
图2:ReLU 函数结果
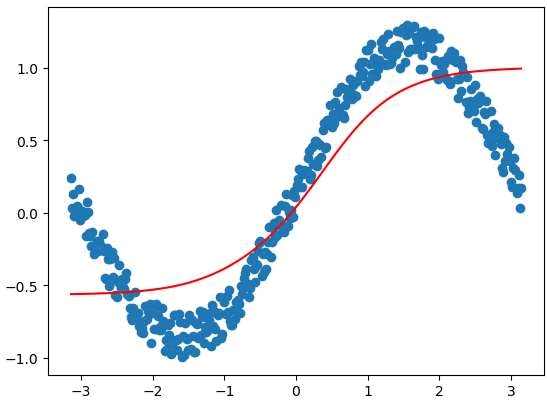
图3:tanh 函数结果
声明:《Python系列教程》为本站“54笨鸟”官方原创,由国家机构和地方版权局所签发的权威证书所保护。
1) 导入必要的模块
这里导入了 sklearn.neural_network 中的 MLPRegressor 回归模块。下面的测试并没有使用 sklearn 中的数据集,而使用模拟的数据。In [1]: import numpy as np ...: import matplotlib.pyplot as plt ...: from sklearn.neural_network import MLPRegressor
2) 生成模拟的自变量数据集
这里生成的是从 -3.14 到 3.14 区间里平均分割的 400 个点。In [2]: X = np.linspace(-3.14, 3.14, 400)
3)转换数据类型
将 X 转换为一个一维的数组。In [3]: X1 = X.reshape(-1,1)
4) 生成模拟的目标变量数据
In [4]: y = np.sin(X) + 0.3*np.random.rand(len(X))
5) 初始化模型对象
In [5]: clf = MLPRegressor(alpha=1e-6,hidden_layer_sizes=(3, 2), random_state=1, max_iter=100000,activation='logistic') # 创建模型对象
6) 训练模型对象
In [6]: clf.fit(X1, y) # 训练模型
Out[6]:
MLPRegressor(activation='logistic', alpha=1e-06, batch_size='auto',
beta_1=0.9, beta_2=0.999, early_stopping=False, epsilon=1e-08,
hidden_layer_sizes=(3, 2), learning_rate='constant',
learning_rate_init=0.001, max_iter=100000, momentum=0.9,
nesterovs_momentum=True, power_t=0.5, random_state=1, shuffle=True,
solver='adam', tol=0.0001, validation_fraction=0.1, verbose=False,
warm_start=False)
7) 预测
In [7]: y2 = clf.predict(X1) # 做出预测曲线
8) 画出预测结果
结果如图 1 所示。In [8]: plt.scatter(X,y)#画图 ...: plt.plot(X,y2,c="red") Out[8]: [<matplotlib.lines.Line2D at 0xaefeeb8>]

图1:回归神经网络结果

图2:ReLU 函数结果

图3:tanh 函数结果
声明:《Python系列教程》为本站“54笨鸟”官方原创,由国家机构和地方版权局所签发的权威证书所保护。
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: