逻辑函数详解
逻辑函数(Logistic Function)又称为 Sigmoid 函数:
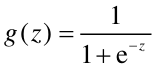
它的特性是所有值都在 (0,1) 之间,如图 1 所示。
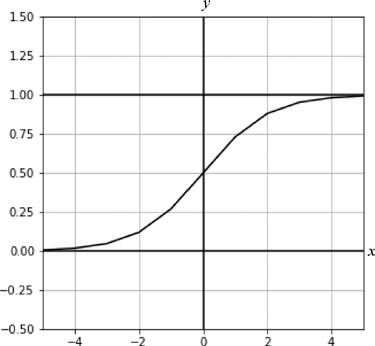
图1:Sigmoid函数
逻辑函数的作用是判断不同属性的样本属于某个类别的概率。在二分类过程中,用1表示正向的类别,用0表示负向的类别,也就是说经过Sigmoid函数转换,如果值越靠近1则其属于正向类别的概率越大;如果值越靠近0,则其属于负向类别的概率越大。
如图 2 所示,点(2,) 经过 Sigmoid 函数激活后的值为 0.88。从图 2 中可以明显看到,该值靠近直线 y=1,也就是说它属于类别 1 的概率大。
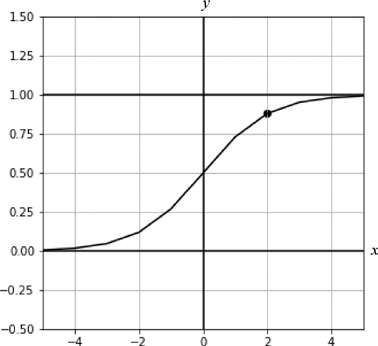
图2:点(2,)
如图 3 所示,点 (-2,) 经过 Sigmoid 函数激活后的值为 0.12。从图 3 中可以明显看到,该值靠近直线 y=0,也就是说它属于类别 0 的概率大。也就是说,该点属于 y=1的概率很小,只有 0.12。相反,该点属于 y=0 的概率有 0.88。
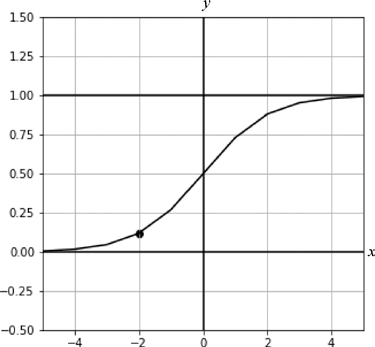
图3:点(-2,)
最后,我们来看 0 值,如图 4 所示。点 (0,) 经过 Sigmoid 函数激活后的值为 0.5。从图 9.11 中可以明显看到,该点与直线 y=0 和直线 y=1 的距离相同,说明该点属于两者的可能性相同,也可以说该点既可能属于类别 1,也可能属于类别 0。
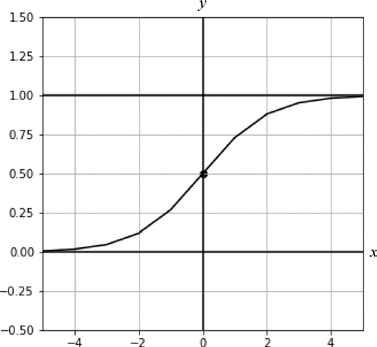
图4:(0,0)
还可以看到当x的绝对值大于 5 时,函数值将无限接近直线 y=1 和直线 y=0,如图 5 所示:
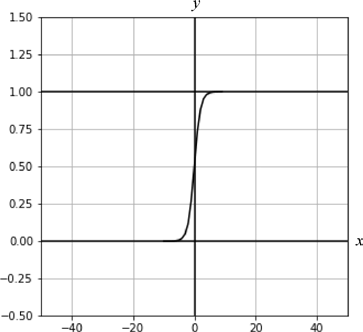
逻辑回归就是将逻辑函数用在线性回归函数上层,将回归问题转换成分类问题。
声明:《Python系列教程》为本站“54笨鸟”官方原创,由国家机构和地方版权局所签发的权威证书所保护。
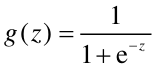
它的特性是所有值都在 (0,1) 之间,如图 1 所示。

图1:Sigmoid函数
逻辑函数的作用是判断不同属性的样本属于某个类别的概率。在二分类过程中,用1表示正向的类别,用0表示负向的类别,也就是说经过Sigmoid函数转换,如果值越靠近1则其属于正向类别的概率越大;如果值越靠近0,则其属于负向类别的概率越大。
如图 2 所示,点(2,) 经过 Sigmoid 函数激活后的值为 0.88。从图 2 中可以明显看到,该值靠近直线 y=1,也就是说它属于类别 1 的概率大。

图2:点(2,)
如图 3 所示,点 (-2,) 经过 Sigmoid 函数激活后的值为 0.12。从图 3 中可以明显看到,该值靠近直线 y=0,也就是说它属于类别 0 的概率大。也就是说,该点属于 y=1的概率很小,只有 0.12。相反,该点属于 y=0 的概率有 0.88。

图3:点(-2,)
最后,我们来看 0 值,如图 4 所示。点 (0,) 经过 Sigmoid 函数激活后的值为 0.5。从图 9.11 中可以明显看到,该点与直线 y=0 和直线 y=1 的距离相同,说明该点属于两者的可能性相同,也可以说该点既可能属于类别 1,也可能属于类别 0。

图4:(0,0)

逻辑回归就是将逻辑函数用在线性回归函数上层,将回归问题转换成分类问题。
声明:《Python系列教程》为本站“54笨鸟”官方原创,由国家机构和地方版权局所签发的权威证书所保护。
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: